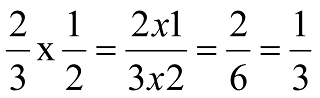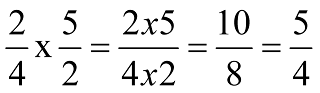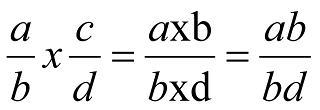Way to find GCD

Way to find GCD

Way to find GCD - In before post maticschool discuss about how to find greatest common divisor. Now maticschool will proves the second way in before post with problem a larger number.

Way ...

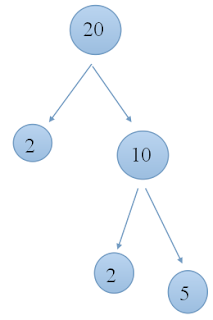
In the second way yesterday we use factor trees to find the gcd. And now maticschool will proves second way in before post with problem a larger number is 100 and 75.

First we determine the two factors with the factor tree.

 

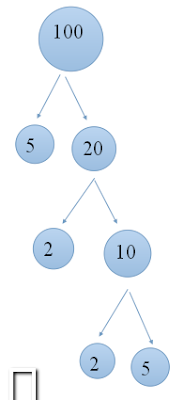
Factor of :  100 : 22, 52 | 75 : 3, 52 

After we know the factors of both. We find the same factors of both these two factors, from these two factors was the same number 5. Then we find the smallest number whose value from the second number 5. Since both number five of the two factors of equal value is 52 . So gcd 100 and 75 is  52 = 25.

By using the first way that we described yesterday will also find the same answer is 25.

With the first way.

Factor from :

       75 : 1, 3, 5, 15, 25, 75,
       100 : 1, 2, 4, 5, 10, 20, 25, 50, 100

From those two factors there are the same number. 

        75 : 1, 3, 5, 15, 25, 75,
        100 : 1, 2, 4, 5, 10, 20, 25, 50, 100

Numbers 1, 5, 25 is a factor from both numbers are the same but Greates common divisor is the greatest number that can divide two numbers are depleted. SO the result is 25. 

Read More

How to fing Greatest Common Divisor

Greatest Common Divisor

Greatest Common Divisor - Greates Common Divisor (GCD), also known as the greatest common factor (gcf) or highest common factor (hcf).

What is Factor ? 
      Factor is a number that can divide other numbers depleted numbers. For more details you can read this example.

         Factors of 20: 1, 2, 4, 5, 10, 20

Numbers 1, 2, 4, 5, 10, and 20 is a factor of 20. Why ? Because of these numbers can divide out the number 20.

What is Greatest Common Divisor ? 
       After we know what that factor ? Then we will understand the meaning of Greatest Common Divisor. Greatest Common Divisor  involve at least 2 numbers. Then what is gcd ? Greates common divisor is the greatest number that can divide two numbers are depleted. For more Details you can further reading this post.

                                                how gcd of 20 and 25 ?

For answer the question above maticschool have some way to answering the questions above.

 Some Way .....
        
1. First way. In this first way we will find the gcd by finding factors of both numbers.

              20 : 1, 2, 4, 5, 10, 20

              25 : 1, 5, 25

Remember ! What is GCD ? Gcd is the greatest number that can divide both numbers are depleted. From a factor of 20 and 25 can be seen that there are several factors that have in common. 

           20 : 1, 2, 4, 5, 10, 20

           25 : 1, 5, 25

From these data it can be seen that the numbers 1 and 5 are both owned by 20 and 25, but Gcd is the greatest number that can divide two numbers are depleted. So from these data it can be concluded that the gcd is 5. However, using such means will be relatively very long to find the gcd of two large numbers.

2. Second Way. The second way we will use the relative does not take much time. In second way we will use factor tree for find the gcd. Still with the same problem we will solve this second way. 

 

From factor tree can be concluded :
   

     25 : 52 | 20 : 22, 5

From the above results there are two numbers that equal the number 5, but with different values​​. Because there are two numbers are the same, we take the smallest value of the 5 factors of 20. Because it only has 1 factor are the same so that's the answer is 5

for proof of the second way you can click here

Read More

Multiplication in Fractions

Multiplication in Fractions

Multiplication in Fractions - Every day we will surely find fractions. Because that we must learn about it And in this post maticschool can discuss through an example.

From two example above it can be concluded that the multiplication of fractions not much different integers. 

Read More

Using Factor Tree in Math

Use Factor Tree in Math  

Factor tree has many functions in mathematics. Besides for find factor the number, factor tree can use for find gcd or lcm in math. And in this discussion maticschool want to discuss how to use the factor tree in math.

Before we use factor tree we must know about primes number. Why ? Because of primes is what will we use for factor tree. To use a factor tree we know of at least between 1-20.

prime numbers between 1-20 = 2, 3, 5, 7, 11, 13, 17, 19

Aftere we know prime numbers between 1-20. Maticschool will give an example with numbers 42.

So from factor tree above the factor of 42 is 2, 3, and 7

Note :
 - In the left position like 2 and 7 is divisor
- Divisor must prime numbers
- In the right position like 21 and 3 is results number
- Factor tree finish if the result number is prime number like in the example is 3

Read More

How to Find Least Common Multiple ( LCM )

Least common multiple

Least common multiple - Least common meultiple is a multiple of two or three ( actually four, five and so on was not anything ) numbers are the same and the smallest. As so of the two numbers 2 and 3. Least common multiple form 2 and 3 is 6. And number 6 multiples 2 and 3. Because number 6 multiples 2 and 3 so number 6 can be divided by 3 and 2. 

The Formula ...

There are many ways to find Leas common multiple. 

1. The first way is by adding two numbers with itself continuosly.

   

     2 : 4, 6, 8, 10, 12, 14, ....                                                                                                               3 : 6, 8, 12, 15, 18, 21, .....  

  

        From the example several multiples from 2 and 3 is same. The same numbers is 6 and 12. But in least common multiple just smallest number called least common multiple. But with this way we will use a long time. 

2. The second way is we will use the factor tree. What is factor tree ? factor tree is like this. 

With factor tree we can find the factor with easy. Because that we will use this. 

Example with factor tree. 

 

Factor from 20 and 25. 

    20 : 22, 5  |  15 : 52 

From two factor of 20 and 25, there are the same number is 5. From both the number five we can look 5 from 20 and 52 from 25. Because there are two same numbers we will take the largest. From two 5 number the largest is 52. Then factor from 20 are 22 we will take this for later. So the  two number we take is 52 and 22. From the number we take we will multipliying the two number. 

       

                                      52 × 22 = 25 × 4 = 100

   So the least common multiple from 20 and 25 is 100 

Proving 

     From the second way we can proving about the second way with the first way. The first way is by adding two numbers with itself continuosly. So...

 25 : 25, 50, 75, 100, 125, 150, 175, 200,....

                                           20 : 20, 40, 60, 80, 100, 120, 140, 160, 180, 200,...

            

From two factor above we can look the same number.

                                            25 : 25, 50, 75, 100, 125, 150, 175, 200,....

                                            20 : 20, 40, 60, 80, 100, 120, 140, 160, 180, 200,...

The same number is 100 and 200 but least common cultiple is a multiple of two or three numbers are the same and the smallest. So the smallest is 100. 

So....

    So from the proving above we can conclude that use first way and second way the result is same. And with use the second way is an effective way and does not take a much time.

Read More

Software for Geometric Learning

Software for Geomtric Learning

Software for Geomtric Learning - May, when we learn in math sometimes difficult understand about geometry. Then we need a way to be more easyly. With this software we can to be more easly understand about geometry. In this software includes a lot of features. In this software we can know where is location of the point, we can draw tangent to circle, can easily draw a circle, etc.

The software name is GeoGebra. Geogebra name comes from geometry and algebra. To download this software you can click here.

Some screen shoot from maticschool :

Read More

Download GeoGebra 4.2.6

Download GeoGebra 4.2.6

Download GeoGebra 4.2.6 - This software will help you when you learn math. Especially when you learn about algebra and geometry. Plus this software is open source. Then this software can used in a variety of operating systems. The operating systems is windows, mac, ubuntu, debian, and other linux, java webstar, android and etc. Next this software do not need a good computer.

This is a some screen schoot from maticschool :

To download you can click here

For windows : size         : 29 mb
                      extension : .exe
                      password : no password

Read More

Division in Fractions

Division in Fractions

Division in Fractions- In before post, maticschool  discuss about multiplication in fractions. And in this post, maticschool  will post about division in fractions. May in division in fractions not to hard like division in integers. Because division in fractions will use multiplication in it.

Formula for Division in Fractions : 

From that formula we can work on the probelm in division in fractions.

For example : 

Keyword for this post : 

division of fractions

division fractions

Read More